电子产品世界

本文探讨了尺寸共振对高频铁氧体磁芯磁场分布的影响。

在本系列的前一篇文章中，我们了解了涡流如何降低大型高频磁芯的频率响应。我们还提到了另一种现象，即维度共振，它会限制带宽并增加这些核心的损耗。在本文中，我们将像研究涡流一样研究维度共振。

传播速度和波长

尽管涡流和尺寸共振都会改变大型磁芯中的场分布，但它们是通过完全不同的机制实现的。为了理解维度共振效应，我们首先需要回顾电磁学的一些基本原理。

从我们的大学课程中，我们知道电磁波在材料内的传播速度由下式给出：

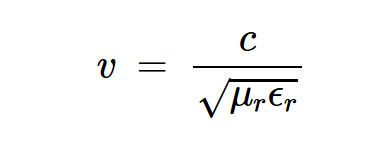
方程式1。

解释：

c是真空中的光速

μr是材料的相对磁导率

εr是材料的相对介电常数。

传播速度是波在介质中传播的速度。例如，在μr=1和εr=1的材料中，传播速度等于真空中的光速。然而，如果磁性材料的磁导率为μr=100，那么材料内部的波速是自由空间中的十分之一。

注意到波在一个周期内传播一个波长的距离，我们可以很容易地推导出传播速度、波长（λ）和频率（f）之间的以下关系：

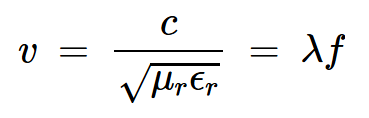
方程式2。

上述方程表明，在给定频率下，波长与速度成正比。例如，如果磁性材料的磁导率为μr=100，那么材料内部的波速和波长都是真空中的十分之一。正如我们即将看到的，这些短波长会对高频磁性元件产生不利影响。

什么是维度共振？

铁氧体的主要优点是其低导电性，这意味着涡流的损耗较小。然而，这些材料的分子结构也可能导致高介电常数。例如，MnZn芯的相对介电常数约为104。NiZn芯通常具有较小的相对介电常数，在其可用频率范围内为100至10。

由于MnZn芯可以在kHz到MHz的频率范围内同时呈现高磁导率和介电常数，因此这些材料中的传播波长可以明显短于自由空间。例如，假设对于某种铁氧体材料，在f=1 MHz时μr=1000，εr=100000。方程式2显示，波长从自由空间中的约300m减小到材料内部的3cm。

在高频（甚至低频，如果磁芯足够大）下工作的磁芯内的波长可能与磁芯的横截面尺寸相当。当这种情况发生时，铁芯横截面的不同点会经历不同的磁场值。换句话说，横截面上的场分布并不均匀。

铁芯的横截面垂直于磁场。当纤芯横截面的一个维度等于半波长时，纤芯将支持驻波。这被称为尺寸共振。

图1显示了尺寸共振如何影响高磁导率圆柱形芯横截面上的场分布。假设芯是无损的，直径为50毫米（a=50），介电常数为150000。

由于尺寸共振，圆柱形芯内的场分布在高频下发生了显著变化。

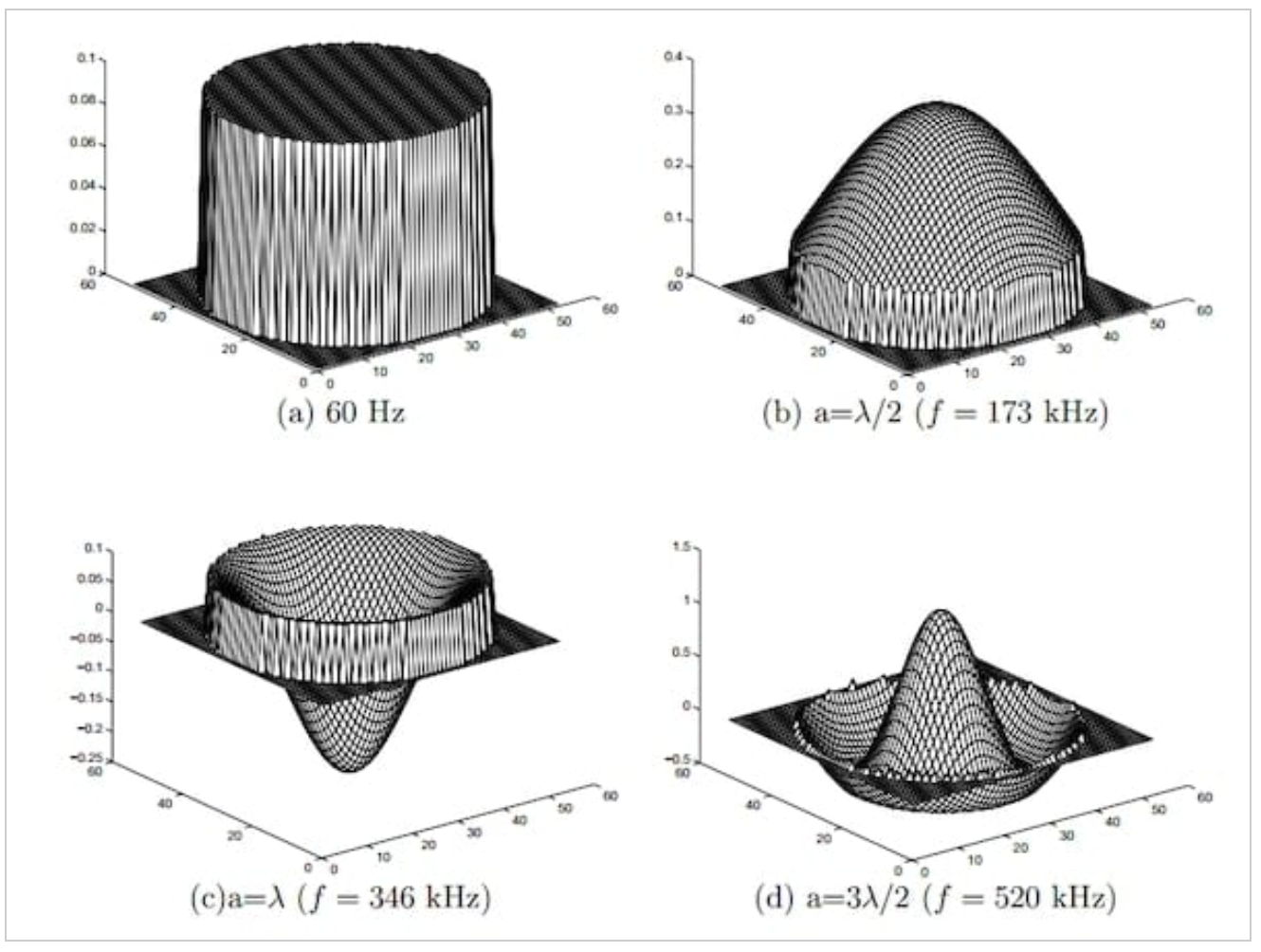
图1。表现出尺寸共振的圆柱形芯的场分布。图片由G.R.Skutt提供

在这些模拟中，铁芯暴露在由均匀缠绕的线圈产生的均匀磁场中。仿真显示了线圈中正弦电流达到峰值时的场分布。

在图1（a）中，频率太低，无法发生尺寸共振。铁芯内的磁通量是均匀的，与励磁电流同相。

然而，随着频率的增加，波长相应地减小。在图1（b）中，它已经减小到半个波长等于芯直径（a=λ/2）的点。正是在这一点上发生了维度共振，产生了与我们在图1（a）中看到的完全不同的场分布。当频率进一步增加时，场分布继续变化，如图1（c）和图1（d）所示（分别为a=λ和a=3λ/2）。

MnZn和NiZn材料的尺寸共振

NiZn材料的磁导率和介电常数远低于MnZn材料。因此，与具有相同横截面尺寸的MnZn芯相比，NiZn芯将在更高的频率下开始表现出尺寸共振。对于典型射频应用中使用的NiZn芯，尺寸共振往往接近1 GHz。

图2给出了MnZn和NiZn材料的共振尺寸的一些典型值。

两种MnZn铁氧体材料和一种NiZn材料的共振尺寸与频率的关系。w

图2:典型MnZn和NiZn材料的共振尺寸。图片由M.Kącki提供

对于给定的工作频率，NiZn材料的共振尺寸远大于MnZn芯的共振尺寸。为了防止材料中驻波的形成，芯的最小横截面尺寸应小于尺寸共振波长的一半。

涡流与尺寸共振的联合效应

趋肤效应和尺寸共振是两个独立的现象，因此在理论上可以分别进行模拟和分析。然而，由于这两种效应可以在真实世界的磁芯中同时发生，因此通过实验隔离这两种效果并针对特定材料独立评估它们可能是不可行的。图3显示了当这两种效应同时发生时的整体场分布。

由于趋肤效应和尺寸共振引起的圆柱形芯的场分布变化。

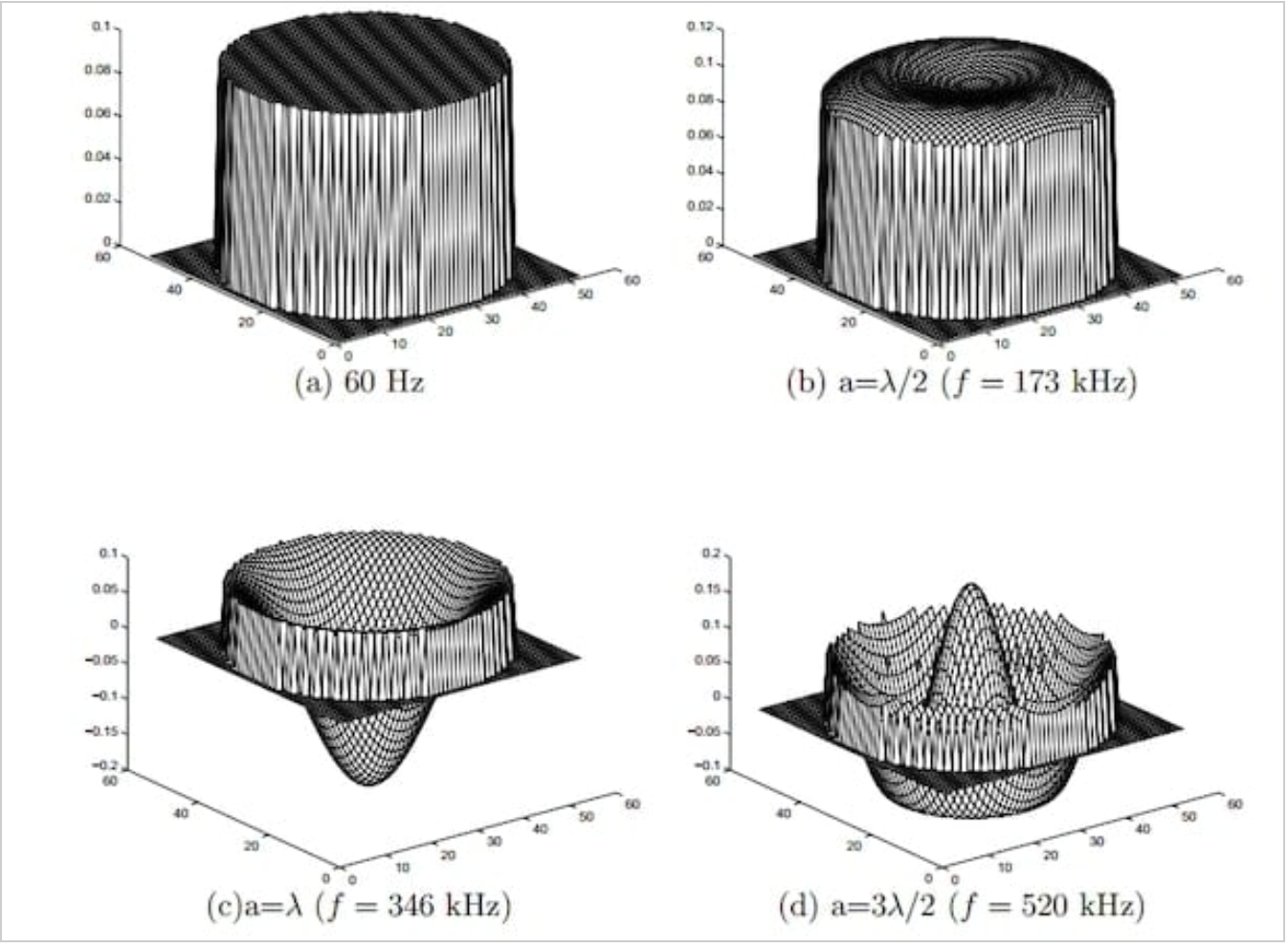
图3。由于趋肤效应和尺寸共振引起的场分布。图片由G.R.Skutt提供

图3中的核心与我们在图1中检查的核心具有相同的尺寸，并且在相同的四个频率下进行了模拟。图1仅考察了尺寸共振的影响——然而，在这组模拟中，材料的电导率被设置为高值，从而也产生了趋肤效应。

通过比较图1（b）和图3（b），我们可以观察到，包括涡流是如何提高堆芯表面附近的通量密度并降低中心的通量密度的。通量密度的这种变化是趋肤效应的特征，在a=λ和a=3λ/2的场分布中也很明显。在a=3λ/2的模拟中，这尤其引人注目。

材料特性的不同组合如何影响场分布

现在我们对磁性材料中的涡流和尺寸共振有了基本的了解，让我们来看看我们对材料的选择如何影响磁芯横截面中的场分布。例如，我们将在500 kHz的频率下检查具有以下尺寸的无损环形磁芯：

外径为90毫米。

内径为60毫米。

高度为20毫米。

最简单的情况是材料具有：

低电导率（σ=0.1S/m）。

低介电常数（εr=1）。

高渗透性（μr=10000）。

该岩心的模拟场分布如图4所示。

低电导率、低介电常数和高磁导率的环形磁芯的磁场分布。

图4。μr=10000，εr=1，σ=0.1 S/m的场分布。图像由m.Kącki提供[PDF]

通量分布几乎是均匀的，尽管在核心的内半径和环的外表面之间逐渐减小。这与理想环形中的理论场分布是一致的。

第二个感兴趣的参数组合是：

高电导率（σ=5S/m）。

低介电常数（εr=1）。

高渗透性（μr=10000）。

结果如图5所示。如前所述，模拟频率为500kHz。

具有高导电性、低介电常数和高磁导率的环形磁芯的场分布。

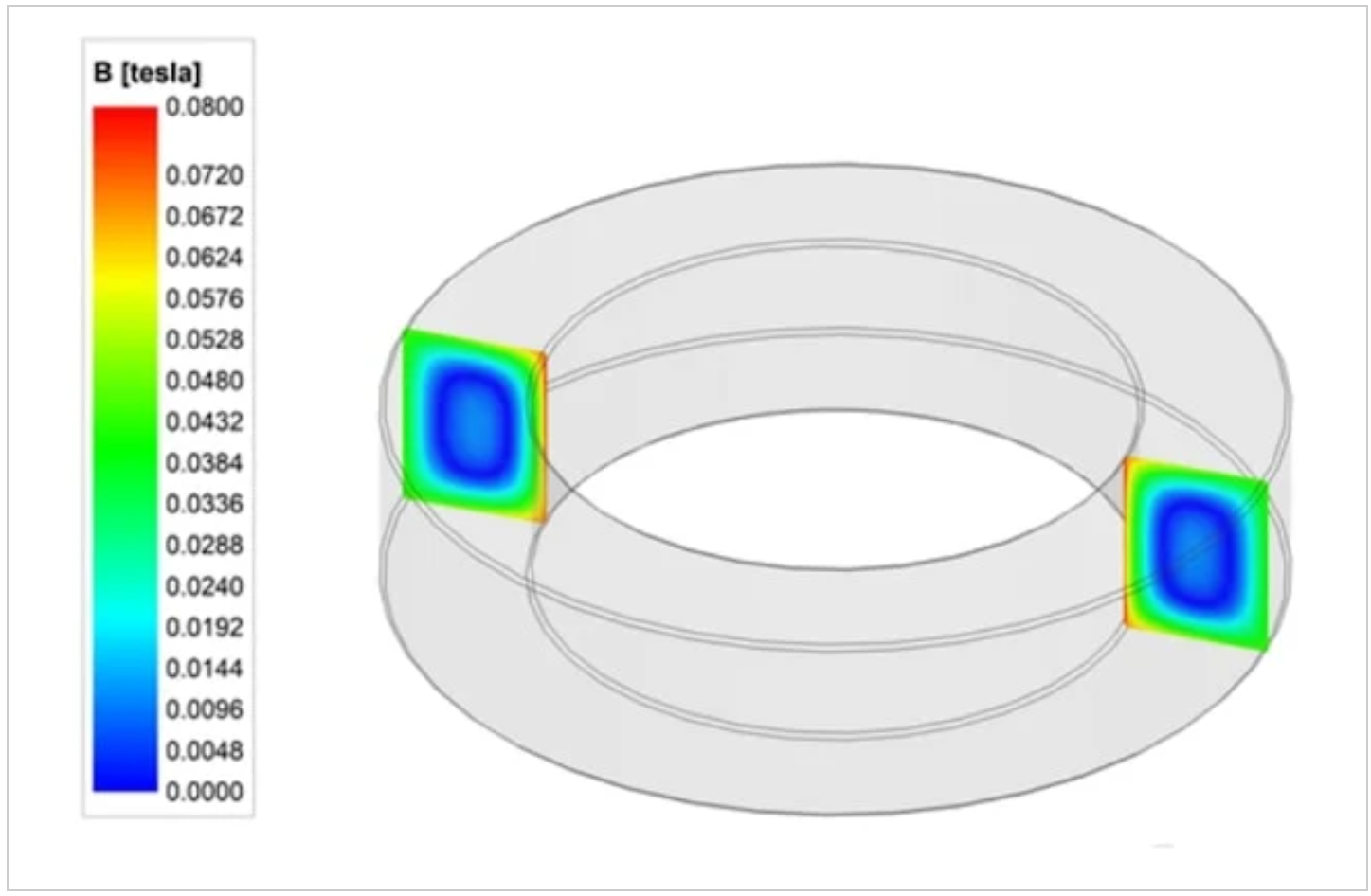
图5。μr=10000，εr=1，σ=5S/m的场分布。图片由m.Kącki提供[PDF]

高导电性和高渗透性的结合导致了较小的趋肤深度。为了您的方便，下面复制了趋肤深度公式：

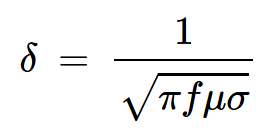
方程式3。

正如我们在本文前面讨论的那样，高介电常数和高磁导率的结合导致了短波长。根据这些参数，波长约为2.6cm，接近芯的横截面尺寸。模拟表明，如预期的那样，通量密度在堆芯中心达到最大值。

如果材料有损怎么办？

在上述讨论中，我们只考虑了无损材料，因此μr和εr被假设为实值。对于有损耗的材料，我们需要使用复磁导率和介电常数值

在波动方程中。在这种情况下，材料中的一半波长由下式给出：

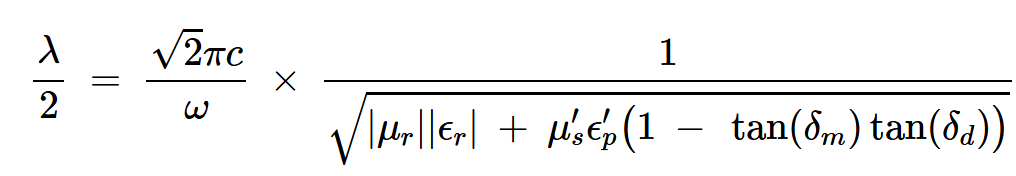
方程式4。

其中分母中的两个损耗角正切项定义为：

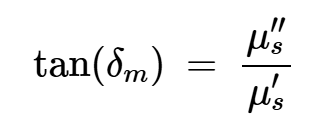
方程式5。

以及：

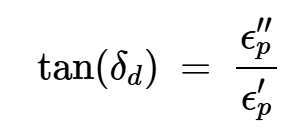
方程式6。

对于有损耗的材料，我们需要考虑两种不同的情况。在一种情况下，tan（δm）tan（δd）远小于1，这意味着材料没有明显的损耗。在这种情况下，方程式4表明波长是一个相对较小的值。因此，可能会发生尺寸共振。

在另一种情况下，tan（δm）tan（δd）远大于单位。因此，我们正在处理一种损耗很大的材料。方程4现在给出了一个大的波长值，这告诉我们核心不能支持驻波。事实上，在这种情况下，衰减是如此之大，以至于场主要集中在核心表面下方的浅层——换句话说，趋肤效应占主导地位。

这种有损耗材料的趋肤深度由下式给出：

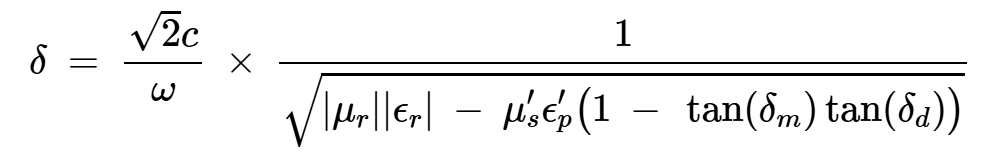
方程式7。

一般来说，我们需要考虑传播波长和材料的趋肤深度，以确定趋肤效应或尺寸共振是否占主导地位，或者这两种效应是否同时存在。

非均匀场的影响

不均匀的磁通分布会导致局部磁饱和。当磁通量分布不均匀时，连接绕组匝数的总磁通量并不简单地与铁芯横截面积成正比。事实上，尺寸共振可以在正负方向上产生等量的磁通量，导致表观磁导率为零。此外，不均匀的场分布会导致更高的损耗。

为了减少尺寸共振的影响，我们必须：

限制操作频率。

使用横截面较小的芯。

我们关于维度共振的讨论到此结束。我希望这篇文章，结合上一篇文章，能帮助你理解高频磁芯中尺寸效应的起源和影响。

关键词： 高频磁芯 尺寸共振